Beskrivelse
I en parallelforbindelse er modstandene placeret parallelt. Når modstandene sidder parallelt betyder det er strømmen i kredsløbet skal dele sig ned gennem begge modstand. Det vil sige at strømmen er den samme indtil den deler sig over modstandene hvorefter strømmen vender tilbage til udgangspunktet når den samles igen.
I en parallelforbindelse er spændingen ens over alle de modstande som sidder parallelt med. Selve leddet af modstande som sidder parallelt, betragtes som én samlet modstand når det gælder spændingsfald.
Måden man gør modstandene op på i en parallelforbindelse er lidt speciel. Når en strøm løber gennem parallelforbundne modstande, så vil strømmen helst løbe igennem der hvor modstanden er mindst. Omvendt, der hvor modstanden er størst løber der mindst strøm igennem. Når strømmen har mulighed for at løbe flere veje over flere modstande så vil den samlede modstand blive mindre end den mindste modstand.
Måden man gør dette på, er ved at omregne den enkelte modstand til dens reciprokke værdi – altså dens omvendte værdi – og lægge den sammen med de andre parallelforbundne modstandes reciprokke værdier. Til sidste tager man de sammenlagte reciprokke værdier og tager det reciprokke af dem. Det vil sige at man laver værdien tilbage til det den var før. Hvis man har gjort det rigtigt så bliver den samlede modstand i de parallelforbundne modstande, mindre end den mindste af de parallelforbundne modstande.
Måden vi skaber den reciprokke værdi af et tal er ved at opløfte tallet i minus første. 2 opløftet i minus første bliver det modsatte af 2 – i forhold til 1 – altså ikke det dobbelte, men det halve.
På samme måde er det reciprokke af 4, en fjerdedel af 1 i stedet for 4 gange 1. Se nedenfor:
eksempel på resiprokke værdier Det lyder måske ret forvirrende, men så slemt er det heller ikke.Formler
Hvis du kun har total R og R2 fx kan du finde R1 ved følgende formel.$$R_1=({1\over {1 \over R}-{1 \over R_2}}) = ({1\over {1 \over 5}-{1 \over 15}})=7,5Ω$$
Eksempel
Et eksempel kan være følgende: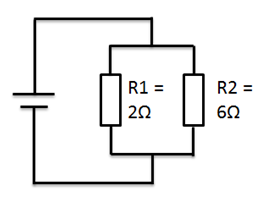
to parallelle modstande
Her ses to modstande som er parallelforbundet. Som sagt ved vi allerede at den samlede modstand, altså R,total, er mindre end den mindste modstand, som er R1 på 2Ω.
Vi regner den samlede modstand ud således: $$R_{tot}=({1\over {1 \over R_1}+{1 \over R_2}}) = ({1\over {1 \over 2}+{1 \over 6}})=1,5Ω$$ R-totalt beregning
Hvis man nu har dobbelt så mange modstande i parallelforbindelser ser det f.eks. således ud:
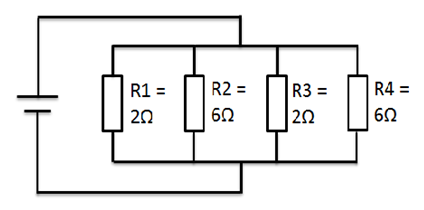
fire parallelle modstande
Dét at der er kommer flere modstande i parallelforbindelsen gør blot den samlede modstand endnu lavere, og altså endnu mindre end den mindste modstand – naturligvis.
Regnestykket ser således ud: $$R_{tot}=({1\over {1 \over R_1}+{1 \over R_2}+{1 \over R_3}+{1 \over R_4}}) = ({1\over {1 \over 2}+{1 \over 6}+{1 \over 2}+{1 \over 6}})= 0,75Ω$$
R-totalt beregning2
Det andre værdier i det første eksempel regnes ud således:
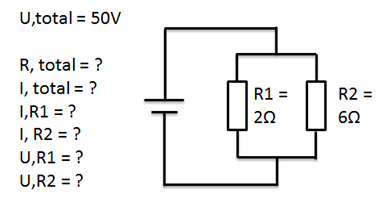
beregning i kredsløb med parallelle forbindelser
beregning R-total og I-total
U,R1 og U,R2 er ens i en parallelforbindelse, spændingen er altså ens ned over begge modstande og man skal betragte hele ledet når man kigger på spændingsfald, men det vil først gøre sig gældende hvis der er flere end en forbindelse.
beregning i kredsløb med parallelle forbindelser2
Kontrol:
beregning i kredsløb med parallelle forbindelser3
HUSK – strømmen er størst over den mindste modstand og omvendt.
Faktisk er der ikke meget mere i parallelforbindelser. Det lidt sværere er når parallelforbindelser sidder i serie med andre parallelforbindelser og enkeltmodstande. Se området blandede forbindelser.